MUL 07

[Note: GERMAN versions of the Week 7 tasks are available HERE. I welcome suggestions on how to improve the translations!]

 In this week's tasks we tint different parts of a shape in different ways and consider ways of determining what fraction of the whole shape has been tinted. We use fairly simply fractions, or fractions that are related in fairly simple ways. 

The tasks provide plenty of scope for adding fractions and for connecting numerical methods to the underlying geometry of the shapes.

Monday: Here we have a rectangle, of which two parts are tinted blue. It turns out that, altogether, ⅓ of the shape is tinted blue.

In Tuesday’s and Wednesday’s version of this task we use geometric methods to solve it. It will be interesting to see whether any students spontaneously use either method here. 

It is likely that students will use some fairly standard numerical method to solve the task, by first expressing the tinted area as 1/4 + 1/12, or perhaps even as 3/12 + 1/12 from the outset. Seeing that the smaller tinted region represents 1/12 involves a fairly simple but nonetheless crucial step of actively partitioning the overall shape into 12 equal regions. Similarly, seeing that 3/12 + 1/12, say, is equal to 4/12 and not 4/24 involves some awareness that when adding fractions we don't just add all corresponding parts.

Tuesday: Here we approach Monday's task in an explicitly geometric way. We partition all the tinted regions into equal-sized parts, just as one would write fractions with the same denominator. But then, instead of adding the numerical fractions, we re-arrange the geometric parts to form a simple single shape (if possible).

We can split the larger tinted region into 4 equal parts, each the same size as the other tinted region, and then move three of these to complete a tinted row along the bottom of the whole shape and occupying ¼ of the whole shape.
Or we could split the smaller tinted region into 4 identical regions using vertical cuts, and then place these against the right hand edge of the other tinted region - but it could be quite a challenge to show that this newly-formed single region covers ¼ of the whole shape.

 

Wednesday: We adopt another geometric approach to Monday's task. This time we initially think of the tinted regions as fractions not of the whole shape but of parts of the whole shape. In our example, the whole rectangle has been split into two parts, A and B say. Then we can state, using the distributive law, that ⅓ of A + ⅓ of B = ⅓ of (A + B) = ⅓ of the whole shape.

A quarter of part of the whole shape + a quarter of the rest of the shape = a quarter of the whole shape.

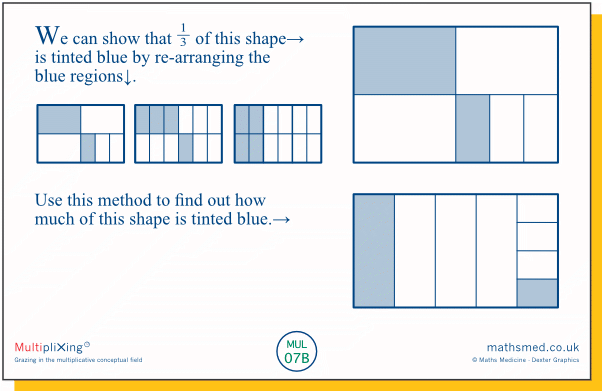
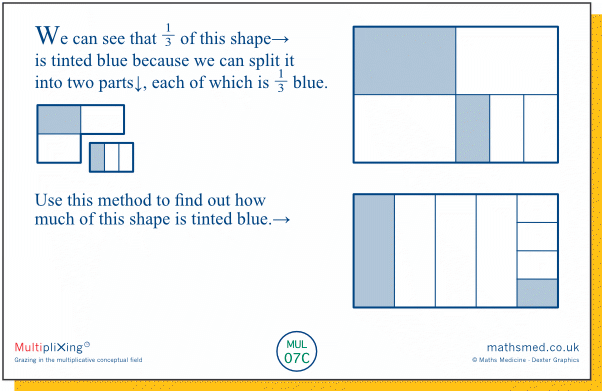
Thursday: Here we have a rather strange but intriguing variant on Wednesday's task, where we partition our shape into more and more, smaller and smaller, parts, each of which is ⅓ blue, except for the smallest part. So at each step, ⅓ of the whole shape is tinted blue, except for the ever smaller part that is still untinted. 

However, instead of analysing the tinted regions in this curtailed, fractions-of-parts-of-the-shape manner, we express each tinted region as a fraction of the whole shape and then add these fractions together. This gives students plenty of practice of seeing fractions as equal parts of a whole, of forming equivalent fractions, numerically and/or by partitioning all the shaded regions into the same equal parts, and of adding fractions once they have the same denominator.

The total tinted amounts form an interesting pattern: ¹⁄₄, ⁵⁄₁₆, ²¹⁄₆₄, ⁸⁵⁄₂₅₆. Can students see how this would continue? The four fractions get ever closer to ¹⁄₃ = ⁵⁄₁₅ = ²¹⁄₆₃ = ⁸⁵⁄₂₅₅.
We can also discern visually that our slanting line of ever-smaller tinted rectangles is matched ever more closely by two slanting lines of ever-smaller untinted rectangles above and below it.

Friday: Here we dispense with tinted shapes and just look at an ever-longer series of fractions. This time the sequence converges on ¼.

The totals are ¹⁄₅, ⁶⁄₂₅, ³¹⁄₁₂₅, ¹⁵⁶⁄₆₂₅.
They get ever closer to ¹⁄₄ = ⁶⁄₂₄ = ³¹⁄₁₂₄ = ¹⁵⁶⁄₆₂₄.
Students might notice that decimals like 0.333... also belong to this kind of fraction series. The denominators of 0.3, 0.03, 0.003, etc, are multiples of 10, but the series converges to 3/9.