Note: GERMAN versions of the Week 18 tasks are available HERE.
This week’s tasks involve the intriguing notion of centre of gravity (CG). This hinges on a simple relation, namely that for two weights, the ratio of their distances from the CG is the inverse of the ratio of the weights themselves. This fits with intuition, in as much as one would expect the CG to be nearer the larger weight.
However, students would benefit from knowing some physics for these tasks, especially the idea of moment of a force about a point, or more loosely for our purposes, moment of a weight about a point, which is proportional to the size of the weight and to its distance from the point. Further, and crucially, if the moments for several weights about a point ‘cancel’ out, the weights are balanced about that point and the point is the centre of gravity.
There isn’t much scope to assess or develop these notions from physics in this limited set of tasks, though a small opportunity to do so is provided in the course of Monday’s introductory task.
However, students would benefit from knowing some physics for these tasks, especially the idea of moment of a force about a point, or more loosely for our purposes, moment of a weight about a point, which is proportional to the size of the weight and to its distance from the point. Further, and crucially, if the moments for several weights about a point ‘cancel’ out, the weights are balanced about that point and the point is the centre of gravity.
There isn’t much scope to assess or develop these notions from physics in this limited set of tasks, though a small opportunity to do so is provided in the course of Monday’s introductory task.
Monday: The main purpose of this task is to introduce the ideas needed for the rest of the week’s tasks, namely centre of gravity and the inverse relation between the ratio of a pair of weights and the ratio of the distances from their centre. As such, the task is rather perfunctory, but you might want to take the opportunity offered by the question, Can you explain why?, to explore and perhaps develop students’ knowledge of moment of a force.
Two identical weights are equivalent to a single weight of twice the size, operating at the point midway between them.
The principle can be applied to unequal weights too, by combining or splitting weights or parts of weights. So, for example, we can find the centre of gravity in the current task by performing the sequence of transformations below.
[Note that at each stage, the sum of the moments about P is zero.]
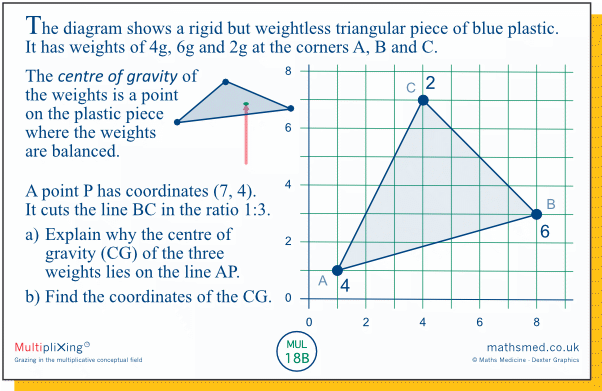
Tuesday: Here we move into 2 dimensions by having three weights in a plane rather than along a rod. However, we can reduce the task to finding successive centres of gravity of pairs of weights connected by a 1 dimensional rod. Thus point P is essentially the centre of gravity of the weights from Monday's task. In turn, the centre of gravity of the three given weights is equivalent to the centre of gravity of the 4g weight at point A and an 8g weight at point P. It will thus cut the line segment AP in the ratio 8:4 or 2:1, which gives us a point with coordinates (5, 3).
The task is quite highly structured, so initially you might want to present it to students without the text, and all its hints, that comes after the second paragraph.
Wednesday: Here we have the same situation as in Tuesday's task, but solve it by pairing the weights in a different order. The eventual solution is of course the same.
After students have solved the task along this alternative route, you might want to suggest that they try solving it a third way, by starting with the weights at A and B. However, this is much more challenging!
Thursday: Here we start with a simple situation of four identical and symmetrically placed weights. We then modify this slightly by increasing one of the weights, which shifts the centre of gravity towards this weight.
When an extra weight is placed at point C, it will be intuitively obvious to some students that the centre of gravity shifts from P to a point closer to C. However, it might be less obvious that we can say with certainty that this new point will lie somewhere on the line segment PC.
In part b) we are told that this new point has coordinates (11, 6). This is quite near C which indicates that the extra weight is quite large....
A neat way of solving part b) is to think of the original four weights as equivalent to a weight of 4g at the point P, so that the extra weight at C becomes the only weight at C. We can then observe that the centre of gravity of the 4g weight and the extra weight at C cuts the line segment PC in the ratio 2:1. This means that these two weights are in the ratio 1:2, and so the mass of the extra weight is 8g.
In part b) we are told that this new point has coordinates (11, 6). This is quite near C which indicates that the extra weight is quite large....
A neat way of solving part b) is to think of the original four weights as equivalent to a weight of 4g at the point P, so that the extra weight at C becomes the only weight at C. We can then observe that the centre of gravity of the 4g weight and the extra weight at C cuts the line segment PC in the ratio 2:1. This means that these two weights are in the ratio 1:2, and so the mass of the extra weight is 8g.
Friday: Part a) of this task is similar to part b) of Thursday's task. A neat way to solve it is treat the configuration of the weights as equivalent to a 4g weight at the centre of the blue square and a 4g weight at C. This, in turn, is equivalent to an 8g weight at (4, 4).
Part b) is quite challenging in that it involves numerous steps. For example, the extra weights at A and D will have a centre of gravity on AD (obviously!) but also on y = 4 (less obviously?). So it is at (1,4). In turn this means the extra weight at D is 3 times the extra weight at A. Also, the total extra weight is half the total weight of the original weights, ie half of 8g. And so on ....